https://natureofchemicalelements.blogspot.com
Wednesday, December 12, 2018
Friday, April 21, 2017
Модель ядра атома, таблица элементов, природа кристаллов и границы применимости квантовой механики.
Во
время учебы в ЛЭТИ познакомился с титанатом бария, который в
зависимости от условий может менять кристаллическую структуру до четырех
разных модификаций. С тех пор и пытаюсь обьяснить механизм этих фазовых
переходов. А попутно исследую и другие свойства химических элементов.
Чтобы досконально разобраться, наверное, необходимо классифицировать
элементы, понять их распределение в таблице элементов. Рассмотреть все
варианты возможных размещений в атоме и ядре протонов, нейтронов и
электронов. Что и сделано в предлагаемой работе.
Модель ядра атома и таблица элементов.
Капельная модель
Была предложена Нильсом Бором в 1936 году в рамках теории составного ядра[1]. Согласно этой теории, атомное ядро можно представить в виде сферической равномерно заряженной капли из особой ядерной материи, которая обладает несжимаемостью, насыщением ядерных сил, «испарением» нуклонов (нейтронов и протонов), напоминая жидкость. Эта модель развивалась Яковом Френкелем и, в дальнейшем, Джоном Уилером, на её основании Карлом Вайцзеккером была получена полуэмпирическая формула для энергии связи ядра атома, названная в его честь формулой Вайцзеккера. Капельная модель является макроскопической теорией, она не учитывает микроскопического строения ядра, например, распределения ядерных оболочек.Модель хорошо описывает важнейшие свойства ядер — свойство насыщения, т.е. пропорциональность энергии связи тяжёлых ядер массовому числу A = N+Z; зависимость радиуса ядра R от A:
Оболочечная модель
Предложена в 1932 году Дмитрием Иваненко совместно с Евгением Гапоном, в 1949 году дополнена Марией Гёпперт-Майер и Хансом Йенсеном. Аналогична теории оболочечного строения атома, в которой электроны наполняют электронные оболочки, и, как только оболочка заполнена, значительно понижается энергия связи для следующего электрона. Согласно модели ядро представляет собой систему нуклонов, независимо движущихся в усреднённом поле, создаваемом силовым воздействием остальных нуклонов. Каждый нуклон находится в определённом индивидуальном квантовом состоянии, характеризуемом энергией, моментом вращения j, его проекцией m на одну из координатных осей и орбитальным моментом вращения l = j± 1/2. Энергия уровня не зависит от проекции момента вращения на внешнюю ось, поэтому на каждом энергетическом уровне с моментами j, l может находиться (2j + 1) нуклонов, образующих оболочку (j, l). Совокупность близких по энергии уровней образует оболочку ядра. Когда количество протонов или нейтронов достигает магического числа, отвечающего заполнению очередной оболочки, возникает возможность скачкообразного изменения некоторых характеризующих ядро величин (в частности, энергии связи). Физической причиной периодичности является принцип Паули, запрещающий двум тождественным фермионам находиться в одном и том же состоянии.Оболочечная модель позволила объяснить спины и магнитные моменты ядер, различную устойчивость атомных ядер, а также периодичность изменений их свойств, применима для описания легких и средних ядер, а также ядер, находящихся в основном состоянии[4].
Модель не объясняет деформированные ядра.
Коллективная модель ядра
Предложена в 1952 году Оге Бором и Б. Моттельсоном. Возникла на основе капельной модели. Рассматривает ядро как остов, образованный нуклонами заполненных оболочек и внешних нуклонов, движущихся в поле создаваемом нуклонами остова. Модель объяснила природу низколежащих возбуждений ядер, которые интерпретируются как динамическая деформация поверхности.Обобщённая модель ядра
Предложена в 1952 году Оге Бором и Б. Моттельсоном. Объяснила большие квадрупольные моменты некоторых ядер тем, что внешние нуклоны таких ядер деформируют остов, который становится вытянутым или сплюснутым.Ротационная модель
Согласно экспериментальным данным в области массовых чисел 150 < A < 190 и А > 200, квадрупольные моменты ядер чрезвычайно велики и отличаются от значений, предсказываемых оболочечной моделью, в десятки раз. В этой же области значений А зависимость энергии нижних возбуждённых состояний ядер от спина ядра оказывается похожей на зависимость энергии вращающегося волчка от его момента вращения. Согласно модели ядро предполагается несферическим.Существенная черта ротационной модели — сочетание вращения всего ядра, как целого, с движением отдельных нуклонов в несферическом потенциальном поле. При этом предполагается, что вращение всего ядра происходит достаточно медленно по сравнению со скоростью движения нуклонов. Ротационная модель позволяет описать ряд существенных свойств большой группы ядер, при этом необъяснённым остаётся сам факт возникновения ротационного спектра (факт вращения всего ядра, как целого).
Модель ядра атома, предложенная нами и таблица элементов.
Каждый последующий химический элемент отличается
от предыдущего тем, что в его ядре количество протонов
увеличивается на единицу, а количество нейтронов растет, в
общем случае, на несколько. В статье предлагается модель ядра
атома, объясняющая это явление.
То есть в ядре всегда больше нейтронов, чем
протонов (не считая самых легких ядер). В литературе это странное
соотношение числа нейтронов к числу протонов для любого ядра
ничем не объясняется.
Для построения модели ядра атома отметим, что при альфа-
радиоактивности ядра гелия имеют примерно равные энергии.
Поэтому на внешней оболочке ядра разместим все протоны с таким
же количеством нейтронов. При этом на одном энергетическом
уровне смогут находиться только бозоны, какими размещенные на
внешней оболочке ядра альфа-частицы и являются. Внутри ядра
расположим оставшиеся нейтроны, задачей которых будет
ослабление электростатических полей отталкивания протонов.
Предположив ядро сферическим, а радиусы протона и нейтрона
примерно одинаковыми, для любого элемента получим модель ядра,
объясняющую отношение числа нейтронов к числу протонов,
вытекающее из упаковки ядра атома нуклонами.
Если массу ядра принять первичной, а химические свойства атома
вторичными, то в таблице элементов атомный вес должен
монотонно изменяться как по горизонтали, так и по вертикали.
Доклады независимых авторов 2005 выпуск №1
173
Построив таблицу по этим признакам, мы вынуждены будем после
лютеция и лоуренсия оставить по четыре пустых места, чтобы
таблица отражала химические свойства элементов - см. табл. 1.
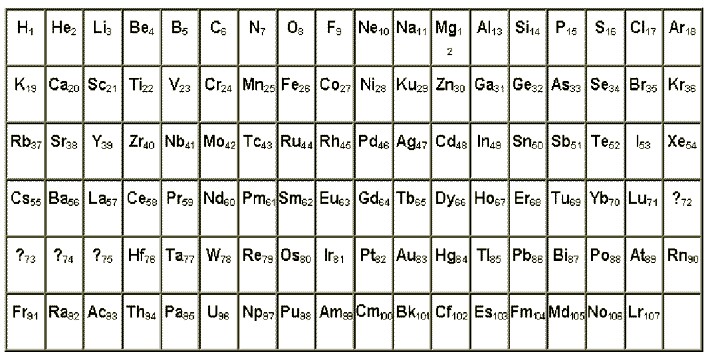
В таблице заполнены все ячейки. У Д.И.Менделеева не таблица, а сложная конструкция. Лантаноиды и актиноиды, которые должны располагаться вертикально согласно их химических свойств, по "домашнему" расположены под таблицей горизонтально.
Антониус Йоханнес ван ден Брук (нидерл. Antonius Johannes van den Broek; 4 мая 1870, Зутермер — 25 октября 1926, Билтховен (нид.)русск.) — нидерландский юрист и физик-любитель. Несмотря на отсутствие специального образования, получил несколько результатов, оставивших след в истории науки. Ему принадлежит первая формулировка положения о равенстве порядкового номера элемента в периодической системе заряду атомного ядра. С именем ван ден Брука связано возникновение ранних теоретических представлений о составе ядра, в частности им была предложена протон-электронная модель ядерного строения. В своих работах он неоднократно пытался найти верный принцип расположения элементов в периодической системе и разработать метод вычисления всех возможных в природе изотопов.
Согласно этой таблице элементов построенной, как по закону Менделеева, а также по правилу ван-Брука, начиная с гафния заряды ядер могут быть на 4 единицы больше, чем принято на сегодня при той же массе.
Построив таблицу, мы вынуждены были после
лютеция и лоуренсия оставить по четыре пустых места, чтобы
таблица отражала химические свойства элементов.
Наверное Джеймс Чедвик сделал ошибку, измеряя заряды ядер атомов.
Точнее не ошибку в измерениях, а в том что согласился с таблицей Менделеева и полученный результат для платины 77,6 был трактован, как заряд ядра равный 78, согласно таблице.
Для меди был получен результат 29,3- больше истинного на 0,3, для серебра 46,3 уже меньше истинного на 0,7, а для платины меньше "истинного" всего на 0,6. Уменьшение связано с экранированием протонов друг другом при измерениях. Поэтому для платины с зарядом 78 результат должен был быть меньше полученного, или другими словами у атома платины заряд ядра больше 78 и равен 82.
Построим модель ядра атома. Знаем что в ядре находятся протоны и нейтроны. В каждом последующем элементе на протон больше, а нейтронов на несколько. Почему? Обьем растет быстрее чем поверхность. При альфа излучении из ядра вылетают ядра гелия примерно одинаковых энергий. Разместив ядра гелия на поверхности ядра атома, получаем с некоторой точностью, что остальные нейтроны находятся внутри ядра. И вопрос а может ли и когда находится внутри ядра протон? Протоны, наверное, начинают размещаться внутри ядра с 72 по 75 элемент, а также со 108 по 111. Пока не открытые элементы.
Периодический закон принадлежит не только в химии, но и в физике.
Прошу повторить опыт Джеймса Чедвика по измерению заряда ядра атома платины. Заряды ядер меди и серебра сомнению не подлежат. Но согласно этой таблице элементов построенной как по закону Менделеева а также по правилу ван-Брука начиная с гафния заряды ядер могут быть на 4 единицы больше чем принято на сегодня при той же массе. Для задания режимов на АЭС, наверное важно знать истинный заряд ядра урана.
Дмитрий Иванович интуитивно чувствовал, что должна быть таблица элементов, а не сложная конструкция, как у него, но ему наверное не хватило знаний по устройству атома и ядра атома. Поэтому лантаноиды и актиноиды у него расположены горизонтально.
таблица элементов, физическая
| H 1 | He 2 | Li 3 | Be 4 | B 5 | C 6 | N 7 | O 8 | F 9 | Ne 10 | Na 11 | Mg 12 | Al 13 | Si 14 | P1 5 | S 16 | Cl 17 | A 1 | |
| K 19 | Ca 20 | Sc 21 | Ti 22 | V 23 | Cr 24 | Mn 25 | Fe 26 | Co 27 | Ni 28 | Cu 29 | Zn 30 | Ga 31 | Ge 32 | As 33 | Se 34 | Br 35 | Kr 36 | |
| Rb 37 | Sr 38 | Y 39 | Zr 40 | Nb 41 | Mo 42 | Tc 43 | Ru 44 | Rh 45 | Pd 46 | Ag 47 | Cd 48 | In 49 | Sn 50 | Sb 51 | Te 52 | I 53 | Xe 54 | |
| Cs 55 | Ba 56 | La 57 | Ce 58 | Pr 59 | Nd 60 | Pm 61 | Sm 62 | Eu 63 | Gd 64 | Tb 65 | Dy 66 | Ho 67 | Er 68 | Tu 69 | Yb 70 | Lu 71 | ? 72 | |
| ? 73 | ? 74 | ? 75 | Hf 76 | Ta 77 | W 78 | Re 79 | Os 80 | Ir 81 | Pt 82 | Au 83 | Hg 84 | Tl 85 | Pb 86 | Bi 87 | Po 88 | At 89 | Rn 90 | |
| Fr 91 | Ra 92 | Ac 93 | Th 94 | Pa 95 | U 96 | Np 97 | Pu 98 | Am 99 | Cm 100 | Bk 101 | Cf 102 | Es 103 | Fm 104 | Md 105 | No 106 | Lr 107 | ||
В квантовой механике
В
квантовой механике по умолчанию в каждом последующем элементе заряд
ядра увеличивается в его центре на единицу и идет заполнение электронами
spdf-конфигураций. У нас заряд ядра расположен на поверхности, т.к.
число протонов и число нейтронов в ядре таковы, что на поверхности ядра
должны быть протоны и нейтроны ,а внутри только нейтроны, то есть на
поверхности ядра образуется некая оболочка. Кроме того протоны должны
отталкиваться, а также их притягивает электронная шуба. Вопрос можно ли
считать в расчетах ядро точкой и до каких пор?
Литература
1. Г. Г. Филипенко. «Подозрительные» области в
периодической системе, "Техника и наука", №4,
Москва, 1990.
2. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", №4, Москва, 1991.
1. Г. Г. Филипенко. «Подозрительные» области в
периодической системе, "Техника и наука", №4,
Москва, 1990.
2. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", №4, Москва, 1991.
Sunday, June 1, 2014
1989г. Гродно.
Природа металлической связи.
Природа кристаллов.
Сейчас,
когда микроэлектроника превратилась в наноэлектронику и грозит перейти в
ангстремэлектронику, важно знать закономерности распределения атомов
(размер атома измеряется в единицах ангстремов) в кристаллической
решетке монокристалла.
Некоторые спрашивают, что, зачем, почему, как.
Основная проблема состоит в том, что используя рентген определили
кристаллические решетки разных материалов, а почему они такие, а не
другие пока не известно. Например медь кристаллизуется в ГЦК решетку, а
железо в ОЦК, которая при нагреве становиться ГЦК-это используется при
термообработке сталей. Медь при нагреве кристаллическую решетку не
изменяет.
В литературе приводится много факторов влияющих на кристаллизацию, поэтому решил их максимально убрать, и модель металла в статье скажем так идеальная, т.е. все атомы одинаковые (чистый металл), без включений, без внедрений, без дефектов и т.д. используя эффект Холла и другие данные по свойствам, а также расчеты Ашкрофта и Мермина , у меня главным определяющим тип решетки фактором оказался остов атома или ион, который получился в результате передачи части электронов в зону проводимости.
Оказалось, что металлическая связь обусловлена не только обобществлением электронов, а и внешними электронами атомных остовов, которые определяют направленность связи или тип кристаллической решетки.
Изменение типа решетки металла может быть связано с переходом электрона в зону проводимости или возвратом его из этой зоны. Фазовый переход.
Думаю, что фазовые переходы возможны и без изменения типа решетки. Медь например. Предполагаю, что в зоне проводимости меди может находиться и один электрон от атома, а может и два.
В литературе приводится много факторов влияющих на кристаллизацию, поэтому решил их максимально убрать, и модель металла в статье скажем так идеальная, т.е. все атомы одинаковые (чистый металл), без включений, без внедрений, без дефектов и т.д. используя эффект Холла и другие данные по свойствам, а также расчеты Ашкрофта и Мермина , у меня главным определяющим тип решетки фактором оказался остов атома или ион, который получился в результате передачи части электронов в зону проводимости.
Оказалось, что металлическая связь обусловлена не только обобществлением электронов, а и внешними электронами атомных остовов, которые определяют направленность связи или тип кристаллической решетки.
Изменение типа решетки металла может быть связано с переходом электрона в зону проводимости или возвратом его из этой зоны. Фазовый переход.
Думаю, что фазовые переходы возможны и без изменения типа решетки. Медь например. Предполагаю, что в зоне проводимости меди может находиться и один электрон от атома, а может и два.
Справочник химика.
Кристаллы металлов строятся из атомов элементов, которые имеют один,
два или три внешних (валентных) электрона (редко больше). При
конденсации металлического пара эти электроны утрачивают связь с
отдельными атомами и обобществляются теми положительными остовами
атомов, которые остаются от них при коллективизации наружных электронов.
Это приводит к образованию связи между системой положительных остовов
атомов в металлической решетке.
| Типы центрировок решёток Браве | ||||
|---|---|---|---|---|
 |  |  |  |  |
| Примитивная | Базоцентрированная | Гранецентрированная | Объёмноцентрированная | Дважды-объёмноцентрированная (Ромбоэдрическая) |
Филипенко Геннадий Григорьевич
К вопросу о металлической связи в плотнейших упаковках
химических элементов
К вопросу о металлической связи в плотнейших упаковках
химических элементов
АННОТАЦИЯ.
Показать начало цитатыОбычно в литературе металлическая связь описывается, как осуществленная посредством обобществления внешних электронов атомов и не обладающая свойством направленности. Хотя встречаются попытки (см. ниже ) объяснения направленной металлической связи т.к. элементы кристализуются в определенный тип решетки.
В работе "К вопросу о металлической связи в плотнейших упаковках химических элементов" показано, что металлическая связь в плотнейших упаковках (ГЕК и ГЦК) между центральноизбранным атомом и его соседями в общем случае, предположительно, осуществляется посредством 9 (девяти) направленных связей, в отличие от числа соседей равного 12 (двенадцати) (координационное число).
Наверное "чужие" 3 (три) атома присутствуют в координационном числе 12 стереометрически, а не по причине связи .Ответ должна дать экспериментальная проверка.
Введение
Пока
невозможно в общем случае вывести из квантовомеханических расчетов
кристаллическую структуру металла по электронному строению атома, хотя,
например, Ганцхорн и Делингер указали на возможную связь между наличием
кубической объемно-центрированной решетки в подгруппах титана, ванадия,
хрома и наличием в атомах этих металлов валентных d- орбиталей. Нетрудно
заметить, что четыре гибридные орбитали направлены по четырем телесным
диагоналям куба и хорошо приспособлены для связи каждого атома с его 8
соседями в кубической объемноцентрированной решетке. При этом оставшиеся
орбитали направлены к центрам граней элементарной ячейки и, возможно,
могут принимать участие в связи атома с шестью его вторыми соседями /3/
стp. 99.
У ОЦК решетки первое координационное число (К.Ч.1) "8" плюс второе координационное число (К.Ч.2) "6" равно "14".
Попытаемся связать внешние электроны атома данного элемента со структурой его кристаллической решетки, учитывая необходимость направленных связей (химия) и наличие обобществленных электронов (физика), ответственных за гальваномагнитные свойства.
Согласно /1/ стр.20, число Z- электроны в зоне проводимости, получено авторами, предположительно, исходя из валентности металла по кислороду, водороду и обязано быть подвергнуто сомнению, т.к. экспериментальные данные по Холлу и модулю всестороннего сжатия близки к теоретическим только для щелочных металлов. ОЦК решетка, Z=1 не вызывает сомнений. Координационное число равно 8.
На простых примерах покажем, что на одну связь у алмаза при плотности упаковки 34% и координационном числе 4 приходится 34%:4=8,5%.
У кубической примитивной решетки плотность упаковки 52% и координационное число 6 приходится 52%:б=8,66%.
У кубической объемноцентрированной решетки плотность упаковки 68% и координационное число 8 приходится 68%:8=8,5%.
У кубической гранецентрированной решетки плотность упаковки 74% и координационное число 12 приходится 74%:12=6.16%, а если 74%:9=8,22%.
У гексагональной решетки плотность упаковки 74% и координационное число 12 приходится 74%:12=6,16%, а если 74%:9=8,22%.
Очевидно, что эти 8,66-8,22% несут в себе некий физический смысл. Оставшиеся 26% кратны 8,66 и 100% гипотетическая плотность упаковки возможна при наличии 12 связей. Но реальна ли такая возможность?
Внешние электроны последней оболочки или подоболочек атома металла образуют зону проводимости. Число электронов в зоне проводимости влияет на постоянную Холла, коэффициент всестороннего сжатия и т.д.
Построим модель металла-элемента так, чтобы оставшиеся, после заполнения зоны проводимости, внешние электроны последней оболочки или подоболочек атомного остова неким образом влияли на строение кристаллической структуры (например: для ОЦК решетки-8 "валентных" электронов, а для ГЕК и ГЦК -12 или 9).
Очевидно, что для подтверждения нашей модели необходимо сравнить экспериментальные и теоретические данные по Холлу, коэффициенту всестороннего сжатия и т.д.
У ОЦК решетки первое координационное число (К.Ч.1) "8" плюс второе координационное число (К.Ч.2) "6" равно "14".
Попытаемся связать внешние электроны атома данного элемента со структурой его кристаллической решетки, учитывая необходимость направленных связей (химия) и наличие обобществленных электронов (физика), ответственных за гальваномагнитные свойства.
Согласно /1/ стр.20, число Z- электроны в зоне проводимости, получено авторами, предположительно, исходя из валентности металла по кислороду, водороду и обязано быть подвергнуто сомнению, т.к. экспериментальные данные по Холлу и модулю всестороннего сжатия близки к теоретическим только для щелочных металлов. ОЦК решетка, Z=1 не вызывает сомнений. Координационное число равно 8.
На простых примерах покажем, что на одну связь у алмаза при плотности упаковки 34% и координационном числе 4 приходится 34%:4=8,5%.
У кубической примитивной решетки плотность упаковки 52% и координационное число 6 приходится 52%:б=8,66%.
У кубической объемноцентрированной решетки плотность упаковки 68% и координационное число 8 приходится 68%:8=8,5%.
У кубической гранецентрированной решетки плотность упаковки 74% и координационное число 12 приходится 74%:12=6.16%, а если 74%:9=8,22%.
У гексагональной решетки плотность упаковки 74% и координационное число 12 приходится 74%:12=6,16%, а если 74%:9=8,22%.
Очевидно, что эти 8,66-8,22% несут в себе некий физический смысл. Оставшиеся 26% кратны 8,66 и 100% гипотетическая плотность упаковки возможна при наличии 12 связей. Но реальна ли такая возможность?
Внешние электроны последней оболочки или подоболочек атома металла образуют зону проводимости. Число электронов в зоне проводимости влияет на постоянную Холла, коэффициент всестороннего сжатия и т.д.
Построим модель металла-элемента так, чтобы оставшиеся, после заполнения зоны проводимости, внешние электроны последней оболочки или подоболочек атомного остова неким образом влияли на строение кристаллической структуры (например: для ОЦК решетки-8 "валентных" электронов, а для ГЕК и ГЦК -12 или 9).
Очевидно, что для подтверждения нашей модели необходимо сравнить экспериментальные и теоретические данные по Холлу, коэффициенту всестороннего сжатия и т.д.
ГРУБОЕ, КАЧЕСТВЕННОЕ ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА
ЭЛЕКТРОНОВ В ЗОНЕ ПРОВОДИМОСТИ МЕТАЛЛА - ЭЛЕМЕНТА.
ОБЪЯСНЕНИЕ ФАКТОРОВ, ВЛИЯЮЩИХ НА ОБРАЗОВАНИЕ ТИПА
РЕШЕТКИ МОНОКРИСТАЛЛА И НА ЗНАК ПОСТОЯННОЙ ХОЛЛА.
(Алгоритм построения модели)
ЭЛЕКТРОНОВ В ЗОНЕ ПРОВОДИМОСТИ МЕТАЛЛА - ЭЛЕМЕНТА.
ОБЪЯСНЕНИЕ ФАКТОРОВ, ВЛИЯЮЩИХ НА ОБРАЗОВАНИЕ ТИПА
РЕШЕТКИ МОНОКРИСТАЛЛА И НА ЗНАК ПОСТОЯННОЙ ХОЛЛА.
(Алгоритм построения модели)
Измерения поля Холла позволяют определить знак носителей заряда в зоне проводимости. Одна из замечательных особенностей эффекта Холла заключается, однако, в том, что в некоторых металлах коэффициент Холла положителен, и поэтому носители в них должны, видимо, иметь заряд, противоположный заряду электрона /1/. При комнатной температуре это относится к следующим металлам:: ванадий, хром, марганец, железо, кобальт, цинк, цирконий, ниобий, молибден, рутений, родий, кадмий, церий, празеодим, неодим, иттербий, гафний, тантал, вольфрам, рений, иридий, таллий, свинец /2/. Решение этой загадки должна дать полная квантовомеханическая теория твердого тела.
Примерно, как для некоторых случаев применения граничных условий Борна-Кармана, рассмотрим сильно упрощенный одномерный случай зоны проводимости. Вариант первый: тонкая замкнутая трубка, полностью заполненная электронами кроме одного. Диаметр электрона примерно равен диаметру трубки. При таком заполнении зоны, при локальном передвижении электрона, наблюдается противоположное движение "места" незаполнившего трубку, электрона, то есть движение неотрицательного заряда. Вариант второй: в трубке один электрон - возможно движение только одного заряда - отрицательно заряженного электрона. Из этих двух крайних вариантов видно, что знак носителей, определяемых по коэффициенту Холла, в какой-то степени, должен зависеть от наполнения зоны проводимости электронами. Рисунок 1.
Рис. 1. Схематическое изображение зоны проводимости двух разных металлов (Масштабы не соблюдены).
а) - вариант первый;
б) - вариант второй.
На порядок движения электронов также будут накладывать свои условия и структура зоны проводимости, и температура, и примеси, дефекты, а для магнитных материалов и рассеяние на магнитных квазичастицах - магнонах.
В приведенной ниже таблице нетрудно заметить, что почти все металлы-сверхпроводники в зоне проводимости содержат по два и более электронов от атома. Это металлы: цирконий, цинк, вольфрам, ванадий, таллий, титан, тантал, рутений, рений, свинец, осмий, ниобий, лантан, иридий, гафний, кадмий, алюминий.
Так как рассуждения наши грубые, учитываем в дальнейшем пока только наполнение зоны проводимости электронами. Заполним зону проводимости электронами так, чтобы внешние электроны атомных остовов оказывали влияние на образование типа кристаллизационной решетки. Предположим, что число внешних электронов на последней оболочке атомного остова, после заполнения зоны проводимости, равно числу атомов соседей (координационному числу) /5/. Координационные числа ГЕК, ГЦК (гексагональной и гранецентрированной) плотнейших упаковок 12 и 18, а объемноцентрированной решетки (ОЦК)8и14/3/.
Построим таблицу с учетом вышеизложенного. Температура комнатная .
| Элемент | RH 1010 (м3/K) | Z.(шт.) | Z остов.(шт.) | Тип решетки | |
| Натрий | Na | -2,30 | 1 | 8 | ОЦК |
| Магний | Mg | -0,90 | 1 | 9 | ГЕК |
| Алюминий или | Al | -0,38 | 2 | 9 | ГЦК |
| Алюминий | Al | -0,38 | 1 | 12 | ГЦК |
| Калий | K | -4,20 | 1 | 8 | ОЦК |
| Кальций | Ca | -1,78 | 1 | 9 | ГЦК |
| Кальций | Ca | T=737K | 2 | 8 | ОЦК |
| Скандий или | Sc | -0,67 | 2 | 9 | ГЕК |
| Скандий | Sc | -0,67 | 1 | 18 | ГЕК |
| Титан | Ti | -2,40 | 1 | 9 | ГЕК |
| Титан | Ti | -2,40 | 3 | 9 | ГЕК |
| Титан | Ti | T=1158K | 4 | 8 | ОЦК |
| Ванадий | V | +0,76 | 5 | 8 | ОЦК |
| Хром | Cr | +3,63 | 6 | 8 | ОЦК |
| Железо или | Fe | +8,00 | 8 | 8 | ОЦК |
| Железо | Fe | +8,00 | 2 | 14 | ОЦК |
| Железо или | Fe | Т=1189K | 7 | 9 | ГЦК |
| Железо | Fe | Т=1189K | 4 | 12 | ГЦК |
| Кобальт или | Co | +3,60 | 8 | 9 | ГЕК |
| Кобальт | Co | +3,60 | 5 | 12 | ГЕК |
| Никель | Ni | -0,60 | 1 | 9 | ГЦК |
| Медь или | Cu | -0,52 | 1 | 18 | ГЦК |
| Медь | Cu | -0,52 | 2 | 9 | ГЦК |
| Цинк или | Zn | +0,90 | 2 | 18 | ГЕК |
| Цинк | Zn | +0,90 | 3 | 9 | ГЕК |
| Рубидий | Rb | -5,90 | 1 | 8 | ОЦК |
| Итрий | Y | -1,25 | 2 | 9 | ГЕК |
| Цирконий | Zr | +0,21 | 3 | 9 | ГЕК |
| Цирконий | Zr | Т=1135К | 4 | 8 | ОЦК |
| Ниобий | Nb | +0,72 | 5 | 8 | ОЦК |
| Молибден | Mo | +1,91 | 6 | 8 | ОЦК |
| Рутений | Ru | +22 | 7 | 9 | ГЕК |
| Родийили | Rh | +0,48 | 5 | 12 | ГЦК |
| Родий | Rh | +0,48 | 8 | 9 | ГЦК |
| Палладий | Pd | -6,80 | 1 | 9 | ГЦК |
| Серебро или | Ag | -0,90 | 1 | 18 | ГЦК |
| Серебро | Ag | -0,90 | 2 | 9 | ГЦК |
| Кадмий или | Cd | +0,67 | 2 | 18 | ГЕК |
| Кадмий | Cd | +0,67 | 3 | 9 | ГЕК |
| Цезий | Cs | -7,80 | 1 | 8 | ОЦК |
| Лантан | La | -0,80 | 2 | 9 | ГЕК |
| Церий или | Ce | +1,92 | 3 | 9 | ГЦК |
| Церий | Ce | +1,92 | 1 | 9 | ГЦК |
| Празеодим или | Pr | +0,71 | 4 | 9 | ГЕК |
| Празеодим | Pr | +0,71 | 1 | 9 | ГЕК |
| Неодим или | Nd | +0,97 | 5 | 9 | ГЕК |
| Неодим | Nd | +0,97 | 1 | 9 | ГЕК |
| Гадолиний | Gd | -0,95 | 2 | 9 | ГЕК |
| Гадолиний | Gd | T=1533K | 3 | 8 | ОЦК |
| Тербий | Tb | -4,30 | 1 | 9 | ГЕК |
| Тербий | Tb | Т=1560К | 2 | 8 | ОЦК |
| Диспрозий | Dy | -2,70 | 1 | 9 | ГЕК |
| Диспрозий | Dy | Т=1657К | 2 | 8 | ОЦК |
| Эрбий | Er | -0,341 | 1 | 9 | ГЕК |
| Тулий | Tu | -1,80 | 1 | 9 | ГЕК |
| Иттербий или | Yb | +3,77 | 3 | 9 | ГЦК |
| Иттербий | Yb | +3,77 | 1 | 9 | ГЦК |
| Лютеций | Lu | -0,535 | 2 | 9 | ГЕК |
| Гафний | Hf | +0,43 | 3 | 9 | ГЕК |
| Гафний | Hf | Т=2050К | 4 | 8 | ОЦК |
| Тантал | Ta | +0,98 | 5 | 8 | ОЦК |
| Вольфрам | W | +0,856 | 6 | 8 | ОЦК |
| Рений | Re | +3,15 | 6 | 9 | ГЕК |
| Осмий | Os | <0 td=""> | 4 | 12 | ГЕК |
| Иридий | Ir | +3,18 | 5 | 12 | ГЦК |
| Платина | Pt | -0,194 | 1 | 9 | ГЦК |
| Золотоили | Au | -0,69 | 1 | 18 | ГЦК |
| Золото | Au | -0,69 | 2 | 9 | ГЦК |
| Таллий или | Tl | +0,24 | 3 | 18 | ГЕК |
| Таллий | Tl | +0,24 | 4 | 9 | ГЕК |
| Свинец | Pb | +0,09 | 4 | 18 | ГЦК |
| Свинец | Pb | +0,09 | 5 | 9 | ГЦК |
Где: RH - Постоянная Холла (коэффициент Холла)
Z - предполагаемое число электронов, отданное одним атомом в зону проводимости
Z остов. - число внешних электронов атомного остова на последней оболочке.
Тип решетки - тип кристаллической структуры металла при комнатной температуре и в некоторых случаях для температур фазовых переходов (T).
Выводы.
Несмотря на грубые допущения, из таблицы видно, что, чем больше атом элемента отдает электронов в зону проводимости, тем положительнее постоянная Холла, и, наоборот, постоянная Холла отрицательна для элементов, отдавших в зону проводимости один-два электрона, что не противоречит выводам Пайерлса , а также просматривается связь между электронами проводимости (Z) и валентными электронами (Zостов), обуславливающими кристаллическую структуру.
Фазовые переходы элемента из одной решетки в другую можно объяснить перебро-сом в зону проводимости металла одного из внешних электронов атомного остова или его возвратом из зоны проводимости на внешнюю оболочку остова под воздействием внешних факторов (давление, температура) .
Пытались дать разгадку, а получили новую, довольно хорошо объясняющую физико-химические свойства элементов, загадку - это "координационное число" - 9 (девять) для ГЦК и ГЕК. Такое частое явление числа-9 в приведенной таблице наводит на мысль, что плот-нейшие упаковки недостаточно исследованы.
Методом обратного отсчета от экспериментальных значений коэффициента всесто-роннего сжатия к теоретическим по формулам Ашкрофта и Мермина /1/, определяя число Z, можно убедиться о его близком совпадении с приведенным в таблице 1.
Металлическая связь представляется обусловленной: как обобществленными элек-тронами, так и "валентными" - внешними электронами атомного остова.
Литература:
1. Н.Ашкрофт, Н.Мермин "Физика твердого тела". Москва, 1979г.
2. Г.В.Самсонов "Справочник "Свойства элементов".Москва, 1976г.
3. Г.Кребс "Основы кристаллохимии неорганических соединений". Москва, l971r.
4. Я.Г.Дорфман, И.К.Кикоин "Физика металлов". Ленинград, 1933г.
5. Г.Г.Скидельский "От чего зависят свойства кристаллов". "Инженер" № 8, 1989г.
Z - предполагаемое число электронов, отданное одним атомом в зону проводимости
Z остов. - число внешних электронов атомного остова на последней оболочке.
Тип решетки - тип кристаллической структуры металла при комнатной температуре и в некоторых случаях для температур фазовых переходов (T).
Выводы.
Несмотря на грубые допущения, из таблицы видно, что, чем больше атом элемента отдает электронов в зону проводимости, тем положительнее постоянная Холла, и, наоборот, постоянная Холла отрицательна для элементов, отдавших в зону проводимости один-два электрона, что не противоречит выводам Пайерлса , а также просматривается связь между электронами проводимости (Z) и валентными электронами (Zостов), обуславливающими кристаллическую структуру.
Фазовые переходы элемента из одной решетки в другую можно объяснить перебро-сом в зону проводимости металла одного из внешних электронов атомного остова или его возвратом из зоны проводимости на внешнюю оболочку остова под воздействием внешних факторов (давление, температура) .
Пытались дать разгадку, а получили новую, довольно хорошо объясняющую физико-химические свойства элементов, загадку - это "координационное число" - 9 (девять) для ГЦК и ГЕК. Такое частое явление числа-9 в приведенной таблице наводит на мысль, что плот-нейшие упаковки недостаточно исследованы.
Методом обратного отсчета от экспериментальных значений коэффициента всесто-роннего сжатия к теоретическим по формулам Ашкрофта и Мермина /1/, определяя число Z, можно убедиться о его близком совпадении с приведенным в таблице 1.
Металлическая связь представляется обусловленной: как обобществленными элек-тронами, так и "валентными" - внешними электронами атомного остова.
Литература:
1. Н.Ашкрофт, Н.Мермин "Физика твердого тела". Москва, 1979г.
2. Г.В.Самсонов "Справочник "Свойства элементов".Москва, 1976г.
3. Г.Кребс "Основы кристаллохимии неорганических соединений". Москва, l971r.
4. Я.Г.Дорфман, И.К.Кикоин "Физика металлов". Ленинград, 1933г.
5. Г.Г.Скидельский "От чего зависят свойства кристаллов". "Инженер" № 8, 1989г.
7. http://natureofcrystalstructure.blogspot.com in English.
ПРИЛОЖЕНИЕ 1.
Оказывается можно кое что прояснить, не привлекая зонную теорию кристалла.
ПРИЛОЖЕНИЕ 2.Металлическая связь в плотнейших упаковках (ГЕК, ГЦК)
Из рассуждений о числе направленных связей (или псевдосвязей, т.к. между соседними атомами металла находится зона проводимости) равном девяти по числу внешних электронов атомного остова для плотнейших упаковок, вытекает, что по аналогии с решеткой ОЦК (восемь атомов-соседей в первой координационной сфере) у ГЕК и ГЦК решеток в первой координационной сфере, должно быть девять, а имеем 12 атомов. Но 9 атомов соседей, связанных любым центральноизбранным атомом, косвенно подтверждаются экспериментальными данными по Холлу и модулю всестороннего сжатия (да и в опытах по эффекту де Гааза-ван -Альфена число осцилляций кратно девяти).
Значит для трех атомов, предположительно из 6 в плоскости шестиугольника (см. рис.1.1) следует искать различия от остальных атомов координационной сферы.
На рис.1.1, d, е показаны координационные сферы в плотнейших гексагональной и кубической упаковках.
Рис. 1.1. Плотные упаковки
Обратим внимание, что в гексагональной упаковке треугольники верхнего и нижнего оснований повернуты в одну и ту же сторону, а в кубической - в разные.
Литература: Б.Ф.Ормонт "Введение в физическую химию и кристаллохимию полупроводников", Москва, 1968 год
.Теоретический расчет модуля всестороннего сжатия (В).
В=(6,13/(rs/а0))5*1010 дн/см2,
где В - модуль всестороннего сжатия,
а0 - боровский радиус,
rs - радиус сферы, объем которой равен объему, приходящемуся на один электрон
проводимости.
rs=(3/4n)1/3,
где n- плотность электронов проводимости.
1. Расчеты по Ашкрофту и Мермину.
Cs Cu Ag Al
2. Расчет по рассмотренным в работе моделям.
Cs Cu Ag Al
Конечно, давление газов свободных электронов само по себе, одно, не полностью определяет сопротивление металла сжатию, тем не менее во втором случае расчета теоретический модуль всестороннего сжатия лежит ближе к экспериментальному, причем с одной стороны. Очевидно необходим учет второго фактора - влияние на модуль "валентных" или внешних электронов атомного остова, определяющих кристаллическую решетку.
Оказывается можно кое что прояснить, не привлекая зонную теорию кристалла.
1996г. Геннадий Филипенко, Гродно
Subscribe to:
Posts (Atom)



